As per my advancement in this topic, I will post a blog here.
The fundamental building block of Linear Algebra is Vector.
So, What the vector is?
There are 3 discrete ideas about vectors, according to the prospective of a Physics, Computer Science and Mathematics.
Physics Perception:
Vectors are arrows pointing in space having a length and direction to define it. In a plane the vector is 2 dimensional and in the space where we live in are 3 dimensional.
Computer Science Perception:
Vector is a ordered list of numbers. It could be considered as the feature of a model. We can represent the vector as a list in computer codes and theories.
A list having length 2 can be seen as 2 dimensional vector and 3 dimensional vector is a list having a length of 3.
Mathematics Perception:
Mathematics has a generalized perception of both view of the vector. Here the vector is an object having a direction and magnitude. And we also can perform arithmetic operation on them like adding two vectors and multiplying numbers to it.
[In this chapter we are going to analyze the vector addition and scalar multiplication in a deliberative manner]
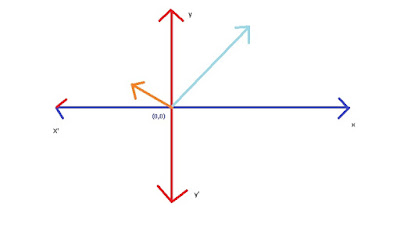
Coming to the beginning, lets consider vector is an arrow inside a coordinate system (x,y plane), where the tail is at the origin (0,0) and the arrow is at the given point. It may be different from the Physics perception (i.e. the vector can be placed anywhere in the plane), but in linear algebra the vector is rooted at the origin.
In 3 dimension we have
In 3 dimension we have another axis present in the coordinate system, i.e. z axis which is parallel to both x and y axis. Each vector associated with all x axis, y axis and z axis.
Vector Addition:
We can take example of a man walking 6 meters from his home and then stopped at a shop. After few minutes he again start walking in same direction for 3 meters. The total distance from current position to his home is 6+3=9. This is an example in a straight line or 1 dimension.
In the same way if we consider the queen movement in a chess board. Lets consider following two moves
- Right up-corner move 2 : (2,2)
- Right 2 : (0,2)
 By taking the 4C as the origin (0,0) of the chess board. The Coordinate of the queen after the first movement (2,2)) will be at 6E and after the second move (0,2) the position of the queen is at 6G.
By taking the 4C as the origin (0,0) of the chess board. The Coordinate of the queen after the first movement (2,2)) will be at 6E and after the second move (0,2) the position of the queen is at 6G.So the total movement is (2+0,2+2)=(2,4).
Scalar Multiplication:
Multiplying a number with a vector is like stretching or squeezing a vector.
Let consider a vector (2,2), that is multiplied with 2
If we have to multiply a negative no with a vector then we just have to flip around the vector and perform the operation.
These process of stretching, squeezing and flipping of the vector is called scaling. Those numbers used for scaling a vector is called as Scalars.







1 comment:
Sign up for the advanced Machine Learning Training in Hyderabad program offered by AI Patasala and work towards getting successfully hired a Machine Learning expert.
Machine Learning Course Hyderabad
Post a Comment